SACRED DRACOMETRY Playing Cards. The mysticism of sacred geometry and dragons

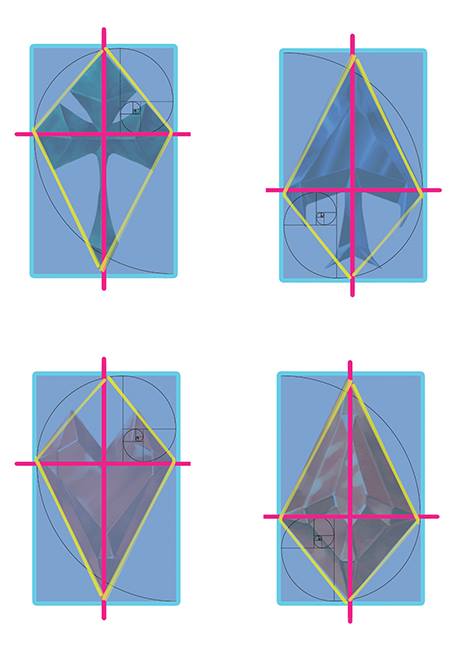
Sacred geometry has historically been interpreted from many disciplines such as philosophy, mathematics or metaphysics. The relationship between geometric forms and nature are present in the culture from the Platonic solids to modern fractals. The presence of sacred geometry elements in the circular magic symbols used to summon dragons inspired Galen Ihlenfeldt, a lover of mythological cultures and graphic fantasy, to illustrate his new deck: SACRED DRACOMETRY.

In its development, Galen has included elements from sacred geometry and each card is full of magical symbolism. Dragon’s eye in the back of the cards emerges from a set of sacred elements with strong symbolic and esoteric value such as the “flower of life” or the “Metatron’s Cube“.

 

 

The court cards show powerful and fearsome dragons framed in fractals and golden symbols.

 

 

 

Numbered cards are built around the geometric representation of each number and also include sacred forms and a dragon’s eye.

 

 

The tuck case shows a real oil painting by Galen for this occasion.

 

 

The cards will be printed by AdMagic, which also printed his previous deck, Deep. Along with the deck, the artist has created other collectibles like dice and a coin.

 

 

This is a really interesting project, with a deep magical inspiration that will strengthen even more the beauty of these cards. If you like it, support the campaign in the project website and raise your pledge.

Good luck!